Nastavnik: Samet Murić
Nastavna jedinica: Pužni parovi osnovni pojmovi i vrste.
Redni br. časa: 76
Tip časa: Obrada
PUŽNI PAROVI
Osnovne karakteristike i podela
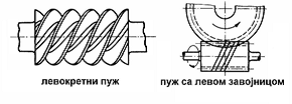
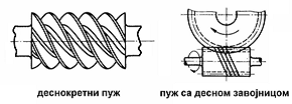
Pužni parovi su hiperboloidni zupčasti parovi čije se ose mimoilaze pod uglom od 90o. Mali zupčanik ”puž” ima oblik navojnog vretena, a veliki zupčanik ”pužni točak” je prilagođen obliku puža. Pri obrtanju puža, koji je u aksijalnom pravcu nepokretan, smer obrtanja pužnog točka zavisi od smera obrtanja puža i pravca njegove zavojnice.
Pužni par sa levom i desnom zavojnicom puža
Jednim pužnim parom mogu se ostvariti veliki prenosni odnosi 5 ≤ u ≤ 50 . Ovako velika redukcija broja obrtaja omogućuje postizanje velikih obrtnih momenata na pužnom točku pri relativno malim obrtnim momentima pogonske mašine. Zato je njihova konstrukcija u poređenju sa cilindričnim i konusnim parovima mnogo kompaktnija. Velika nosivost pužnog para obezbeđuje se istovremenim sprezanjem većeg broja zubaca i dobrim uhodavanjem i podmazivanjem bokova spregnutih zubaca.
Prema obliku temene i podnožne površine puža, pužni parovi se dele na cilindrične i globoidne.
Cilindrični i globoidni pužni parovi
Temena i podnožna površina puža, cilindričnih pužnih parova, ima oblik kružnog cilindra.Kod pužnog točka one su prilagođene podnožnoj i temenoj površini puža i imaju oblik kružnog torusa. Temene i podnožne površine puža i pužnog točka, globoidnih pužnih parova, imaju oblik kružnog torusa.
Geometrijske i kinematske veličine
Analiza oblika spregnutih bokova zubaca i određivanje geometrijskih i kinematskih veličina
pužnog para vrše se u ravni koja je upravna na osu pužnog točka i koja istovremeno
predstavlјa aksijalnu ravan puža. Sprezanje bokova pužnog para može se aproksimirati
sprezanjem ravnog cilindričnog zupčastog para, tj. kotrlјanjem podeonog cilindra pužnog točka po podeonoj ravni ili podeonog kruga po podeonoj pravoj.
Iz uslova kotrlјanja bez klizanja podeonih linija sledi jednakost koraka na podeonom krugu pužnog točka i podeonoj pravoj puža:
p2 = p1 = p = m⋅π
gde je:
m – modul pužnog para
Kao kod zavrtnjeva (vijaka), ugao nagiba navoja definisan je uglom uspona zavojnice na srednjem
cilindru puža:
tg γ = Ph/d m1 π
gde su:
Ph = z1 ⋅ p1 – hod zavojnice puža;
z1 – broj zubaca (broj početaka) puža, z1 = 1…6
dm1 – prečnik srednjeg cilindra puža (deblјina zupca jednaka je širini međuzublјa).
Na osnovu izraza za ugao srednje zavojnice puža, može se odrediti prečnik srednjeg cilindra puža
dm1= z1 m π / π tg γ =m q
q =z γ- predstavlja pužni broj
 SSŠ Rožaje SREDNJA STRUČNA ŠKOLA – ROŽAJE
SSŠ Rožaje SREDNJA STRUČNA ŠKOLA – ROŽAJE
